8.4 RELACION ENTRE EL MOVIMIENTO SINUSOIDAL Y EL CIRCULAR

CONCEPTO DE VELOCIDAD ANGULAR

La velocidad se expresa como la relación que existe entre el espacio recorrido y el tiempo empleado en dicho recorrido.
Si el espacio recorrido es e y el tiempo empleado en recorrerlo es t diremos que la velocidad v = e / t
Si usted recorre con su vehículo una distancia de 144 Km. en 2 horas, podemos decir que su velocidad (media) es de v = 144 / 2 = 72 Km./h.

Del mismo modo, en un movimiento circular, es decir, en aquel cuya trayectoria es una circunferencia, se puede definir de otra manera la velocidad.

Ahora nos interesa, más que el camino recorrido, el ángulo que ha descrito nuestro movimiento durante un tiempo determinado. Y así diremos que si nuestro móvil se traslada a lo largo de la circunferencia un ángulo de 70º en 2 segundos diremos que se ha movido con una velocidad de 70/2 = 35º en un segundo. 
Esta nueva manera de expresar la velocidad se denomina VELOCIDAD ANGULAR.

Dado que la unidad natural del ángulo es el RADIAN (La circunferencia tiene 2 p radianes). La velocidad angular se expresará  en RADIANES POR SEGUNDO (Rad/seg.).

Entonces , si un móvil lleva una velocidad angular w ( por ejemplo, 4 rad/seg.), al cabo de un tiempo t ( por ejemplo, 2 segundos), habrá descrito un angulo (f):
que será igual al producto de la velocidad angular w por el tiempo t:

f = w t = 4 . 2 = 8 radianes

MOVIMIENTO CIRCULAR

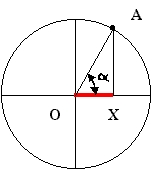Fijaros que al moverse el punto A a lo largo de la circunferencia, proyecta una sombra (roja en la figura) de longitud OX Si llamamos a al ángulo que forman la línea OA con la línea OX se define el coseno del ángulo a como el cociente entre la distancia OX y la distancia OA:               OX cos a =  ------               OA Por lo que podemos decir que OX = OA  cosa

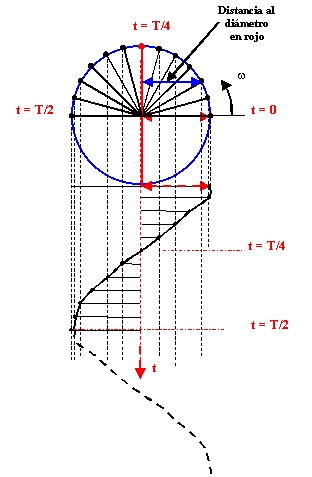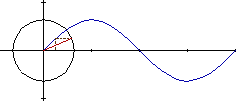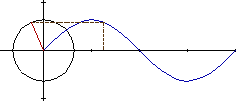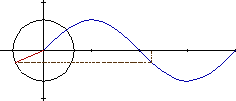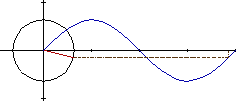
T es el tiempo que tarda el punto en recorrer la circunferencia, a este tiempo le llamaremos periodo Si el punto A se mueve a lo largo de la circunferencia, observamos que: en t=0 la proyección es máxima,  en t = T/4 es nula  y en t=T/2 es máxima pero negativa. Hemos dividido la parte superior de la circunferencia en 12 partes y para cada punto la distancia al eje vertical, la hemos llevado a la parte inferior, y uniendo los puntos obtenemos la curva del coseno. EL MOVIMIENTO SINUSOIDAL ES LA PROYECCION DEL MOVIMIENTO CIRCULAR.

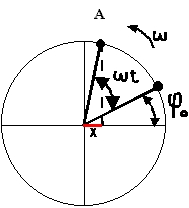
Resumiendo lo dicho: Veamos el radio de amplitud A de la figura, que suponemos que incialmente forma un ángulo j0 con la horizontal y que en cierto momento  comienza a girar con una velocidad w.  Al cabo de t segundos, se habrá desplazado un ángulo w t, por lo que se encontrará formando un angulo f con la horizontal de valor j0 + wt.

La proyección en cada instante del extremo del radio sobre el eje horizontal valdrá :  

x = cos (wt + j₀ )

Sobre el movimiento circular (periódico) se definirán unos conceptos que serán de aplicación en el movimiento sinusoidal:

w = PULSACION : La pulsación del movimiento sinusoidal equivale a la velocidad angular del movimiento circular. Se expresará, por tanto, en radianes por segundo.- (Recordar que una circunferencia tiene 2 p radianes)
T = PERIODO : es el tiempo que tarda el radio en describir una vuelta completa, que es, a su vez, el tiempo que tarda en repetir su valor.
f = FRECUENCIA : Es el número de vueltas por segundo y, por tanto, el número de periodos por segundo.- (Su valor es la inversa de dicho periodo)
j₀ = FASE : Es el ángulo inicial formado por el radio antes de empezar a contar el tiempo. En el movimiento sinusoidal representa el desplazamiento del eje vertical respecto del comienzo de la sinusoide.
A = AMPLITUD  o VALOR MAXIMO de la sinusoide: Es el valor del radio en el movimiento circular
x(t) = VALOR INSTANTANEO. Es el valor de la sinusoide en cada instante. En el movimiento circular es la proyección del radio sobre el eje horizontal

Así pues, hay una relación entre frecuencia, periodo y pulsación. En efecto:
Si para describir una vuelta se necesitan T segundos ( por jemplo T = 0,5 seg.)
¿ Cuántas vueltas describirá en 1 segundo ?
Lógicamente 2 vueltas.
Es decir 
f = 1 / T  o lo que  es  lo mismo T = 1 / f
Cada circunferencia tiene como ya se ha dicho 2 p radianes. Por lo tanto si se describen f vueltas por segundo ( por ejemplo 2 vueltas por segundo) equivale a decir que la velocidad angular es de 2 p . 2 radianes por segundo es decir 4 p rad /s. w = 2 p f = 2 p / T

La frecuencia resulta ser la inversa del período:

       1
f = ---
       T
         1
T = ---
         f