Vamos a ver una serie de circuitos que se van a caracterizar porque procesan señales que sólo tienen dos niveles, y cuyos valores precisos no son importantes con tal que estén en un nivel o en otro de los definidos. Son señales binarias y los circuitos correspondientes se denominan indistintamente, circuitos de conmutación, circuitos lógicos o circuitos digitales

La primera parte de nuestro estudio comprende, primeramente, las bases del álgebra de conmutación, cuya herramienta matemática, el álgebra de Boole, nos va a permitir el análisis y diseño de los circuitos electrónicos digitales.

Seguidamente estudiaremos las familias lógicas o circuitos digitales integrados de que disponemos para nuestras realizaciones.

Por último presentaremos dos grandes bloques: los circuitos y subsistemas combinacionales y los secuenciales. 

• Los primeros se podrán definir como aquellos en que el estado lógico de sus salidas depende únicamente de los niveles de sus entradas en ese mismo instante, es decir no hay efectos de tiempos o memoria. 
• En los segundos, el nivel de salida en un instante dado depende no solamente de las entradas en ese instante, sino del estado interno del sistema, el cual es fruto de las entradas en instantes anteriores, es decir, hay memoria.

Definición: Un conjunto B dotado con dos operaciones algebraicas más (+) y por (.) es un álgebra de Boole, sí y sólo sí se verifican los postulados:

1º  Las operaciones + y . son conmutativas.
2º  Existen en B dos elementos distintos representados por los símbolos 0 y 1, respectivamente, tal que :

a + 0 = 0 + a = a  Para todo elemento a que pertenece a B
a . 1 = 1 . a = a    Para todo elemento a que pertenece a B

3º  Cada operación es distributiva para la otra, esto es:

a + (b . c) = (a + b) . (a + c)
a . (b + c) = (a . b) + (a . c)

4º  Para cada elemento de B, por ejemplo el elemento a, existe un elemento a' también perteneciente a B tal que:

a + a' = 1
a . a' = 0

Ejemplos:
Sea el conjunto B = { 0,1 }, y las dos operaciones + y . definidas

Interruptor abierto 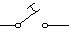  equivale a nuestro 0 lógico
Cerrado 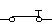   equivale a nuestro 1 lógico
La combinación 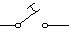 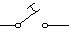  es equivalente a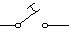 
es decir : dos interruptores abiertos puestos en serie equivale a un solo interruptor abierto

es equivalente a decir en nuestra álgebra de Boole que  0 . 0 = 0

La combinación 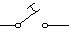 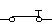 es equivalente a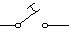 
es decir : un interruptor abierto en serie con un interruptor cerrado equivale a un  interruptor abierto

es equivalente a decir en nuestra álgebra de Boole que  0 . 1 = 0
por la misma razón podemos decir que 1 . 0 = 0

 La combinación 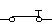 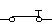 es equivalente a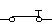 
es decir : un interruptor cerrado en serie con otro cerrado equivale a un  solo interruptor cerrado

es equivalente a decir en nuestra álgebra de Boole que  1. 1 = 1

La combinación 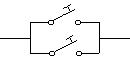   es equivalente a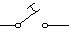 
es decir : dos interruptores abiertos puestos en paralelo equivale a un solo interruptor abierto

es equivalente a decir en nuestra álgebra de Boole que  0 + 0 = 0

La combinación 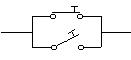   es equivalente a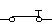 
es decir : un interruptor abierto en paralelo con un interruptor cerrado equivale a un  interruptor cerrado

es equivalente a decir en nuestra álgebra de Boole que  1 + 0 = 0
por la misma razón podemos decir que 0 + 1 = 1

La combinación 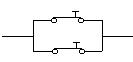   es equivalente a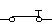 
es decir : un interruptor cerrado en paralelo con un interruptor cerrado equivale a un  interruptor cerrado

es equivalente a decir en nuestra álgebra de Boole que  1 + 1 = 1

Se llama término canónico de una función lógica a todo producto o suma en el cual aparecen todas las variables de que depende esa función. A los términos productos se les llama productos canónicos y a los términos sumas, sumas canónicas.

Cuando una función se expresa como suma de productos canónicos o como producto de sumas canónicas, se dice que dicha función se en cuentra expresada en su forma canónica.

Dos expresiones booleanas, F1 y F2, son equivalentes, es decir F1=F2, sí y sólo sí describen la misma función de conmutación. Comprobaremos que formas booleanas diferentes pero equivalentes, conducirán a circuitos de conmutación distintos aunque realicen la misma función.

La tabla de verdad de una función lógica es una forma de representación de la misma, en la que se indica el valor 0 ó 1 que toma la función para cada una de las combinaciones de valores de las variables de dicha función

Ejemplo:

    a b c    F
0   0 0 0    0
1   0 0 1    1
2   0 1 0    1
3   0 1 1    0
4   1 0 0    1
5   1 0 1    1
6   1 1 0    1
7   1 1 1    1

En la columna de la izquierda se han ido numerando las combinaciones posibles de valores que siempre es igual a 2 elevado al número de variables (n), es decir 2ⁿ, en nuestro caso 2³=8.

De la tabla de verdad de una función lógica, es fácil deducir las formas canónicas de la función. 

Así pues, si queremos que la función F de nuestro ejemplo esté expresada como suma de productos canónicos deberemos asegurarnos que para cada una de las combinaciones de la tabla de verdad en que la función valga 1 obligaremos a que el término canónico valga también 1. Por ejemplo para la combinación a=0 b=0 y c=1 de la tabla de verdad vemos que la función vale 1 así pues nuestro término canónico será a'. b'. c , debemos entender que a' significa que la variable a está negada.

Observemos que el término a'. b'. c vale 1 para la combinación 0 0 1 y sólo para esa combinación, cualquier otra haría que nuestro producto canónico a'. b'. c sea 0.

Construyendo la función con todos sus términos llegaremos a la conclusión que para:

La combinación 010 el término será a'. b. c'
La combinación 100 el término será a . b'. c'
La combinación 101 el término será a . b'. c
La combinación 110 el término será a . b. c'
La combinación 111 el término será a . b. c

Con lo que la función F correspondiente a la tabla de verdad anterior será:

 F = a'. b'. c + a'. b. c' + a . b'. c'+ a . b'. c + a . b . c' + a . b . c

Observemos que tenemos 6 términos que se corresponden con los seis 1 de la función.

Otra forma de expresarla es F = S ( 1, 2, 4, 5, 6, 7 ) S significa suma

F = Sumatorio de términos canónicos en que la función vale 1

También podemos recurrir a realizar la función como producto de sumas canónicas, en este caso nos fijaremos en los 0 de la función y así para la combinación 000 y 011 nuestra función vale 0. Por tanto el término correspondiente a la combinación 000 será ( a + b + c ), y observamos que este término sólo vale 0 para la combinación 000 y para cualquier otra vale 1.Del mismo modo para la combinación 011 el término será ( a + b' + c' ) y observamos también que este término sólo vale 0 para la combinación 011, cualquier otra hará que dicho término valga 1.

Nuestra función expresada como producto de sumas canónicas nos quedará:

F = ( a + b + c ) ? ( a + b' + c' )

Observemos que tenemos 2 términos que corresponden con los dos 0 de la función.

Otra forma de expresarla es F = P ( 0, 3 )   P significa producto

F = Producto de términos canónicos en que la función vale 0

Las tabla de verdad nos permiten comprobar si dos expresiones lógicas distintas son equivalentes, es decir reproducen la misma función de conmutación.

F₁ = a'. b'. c + a'. b. c' + a . b'. c'+ a . b'. c + a . b . c' + a . b . c
F₂ = ( a + b + c ) ? ( a + b' + c' )

Estas dos funciones aparentemente distintas son equivalentes pues ambas tienen la misma tabla de verdad.

1º Para cualquier elemento b del álgebra de Boole se verifica:

b = b + b
b = b . b

Demostración:  Sabemos que (1)  b = b + 0 y que (2)  b . b' = 0
Sustituyendo el 0 de la ecuación (1) por su valor en (2) nos queda que

b = b + b . b'

aplicando la propiedad distributiva no queda entonces 

b = ( b + b ) . ( b + b' )

como   b + b' = 1 entonces

b = ( b + b ) . 1

luego  queda demostrado que b = b + b

2º Para cualquier elemento b perteneciente al álgebra de Boole se verifica:

b + 1 = 1
b . 0 = 0

b + 1 = 1 Esto es lógico ya que si hemos asociado que el valor 1 es equivalente a un interruptor cerrado y el signo + a que los dos elementos b y 1 están en paralelo deduciremos que sea cuál sea el valor de la variable b, si está en paralelo con un interruptor cerrado el resultado eléctrico es que estamos cortocircuitando a la variable b y el resultado será 1.
b . 0 = 0  También es lógico ya que si asociamos 0 como un interruptor siempre abierto y la operación ( . = por ) como que está en serie con el elemento b, el resultado será equivalente a tener siempre un circuito abierto es decir 0.

3º Para cada par de elementos en un álgebra de Boole se verifica

Ley de absorción

a + a . b = a
a . ( a + b ) = a

Demostración : Como a . 1 = a y ( 1 + b ) = 1

a  + a . b = a . 1 + a . b = a . ( 1 + b ) = a . 1 = a

4º  En un álgebra de Boole las operaciones suma, producto son asociativas.

a + ( b + c ) = ( a + b ) + c = a + b + c
a . ( b . c ) = ( a . b ) . c = a . b . c

5º Para cada elemento b en un álgebra de Boole su complemento ( negado) b' es único.