4.4 FUERZA ELECTROMOTRIZ, CONTRAELECTROMOMOTRIZ
Y DIFERENCIA DE POTENCIAL.
El
concepto de diferencia de potencial (d.d.p.) ha sido suficientemente tratado:
Es
la diferencia entre los potenciales de dos puntos de un circuito, y se
expresa en voltios. Se le puede llamar tambien
voltaje o tensión.
Ahora bien,
una diferencia de potencial puede ser producida por dos
causas bien distintas:
-
Una corriente
I, proviniente de algún dispositivo exterior, circula
por una resistencia R, produce en ella
una d.d.p. de valor V = R x I.
Esto se conoce
como CAIDA DE POTENCIAL.
Se dice, por ejemplo, que :
Una corriente
de 2 A. a través de una resistencia de 10 W
produce una caida en sus extremos de 20 V. (V = R x I = 10 x 2 = 20 V).
-
Un generador
produce una d.d.p., y es capaz de entregar
corriente a otros dispositivos.
Esto es, al contrario
que en el caso anterior, una SUBIDA DE POTENCIAL.
Los generadores
crean subidas de potencial que contrarrestan las caidas que se producen
en las cargas (Obsérvese que esto es la 1ª Ley de Kirchoff).
Esta diferencia de potencial producida por los generadores,
capaz de elevar las cargas eléctricas de un potencial a otro
más alto, es lo que se conoce como FUERZA
ELECTROMOTRIZ. La fuerza electromotriz (f.e.m.) de un
generador es la diferencia de potencial que se mide en sus bornes (sus
extremos) cuando está en circuito abierto, es decir, sin suministrar
corriente.
En efecto, cuando se carga un generador, (porque
conectamos por ejemplo una resistencia o cualquier otro tipo de receptor),
circula una corriente.
Esta corriente produce una caida de potencial
en la propia resistencia interna del generador, que se resta de su f.e.m.,
dando como resultado que la tensión presente en bornes del generador
cargado
es menor que su f.e.m.
Recordar :
que la resistencia interna del generador
es una resistencia fictícia, (no existe como tal resistencia en
su interior) sino que el generador se comporta como si la tuviera.
|
Ri = 1 W |
|
|
|
|
+
RL = 4 W
- |
Tensión en vacio = 10
V (f.em.).-Es la tensión entre los puntos A y B cuando RL
no está conectada y por tanto no circula corriente.
|
Entre los puntos A y B y mirando hacia
la izquierda hemos colocado el circuito equivalente a un generador real,
que se compone de un generador ideal de E = 10 V. en serie con una resistencia
(resistencia interna del generador) de valor Ri = 1W
Al conectar la resistencia de carga RL
= 4 W , (ver figura anterior) circulará
una corriente desde el el punto A hacia el B a través de la resistencia
de carga RL de valor: I = E / (Ri + RL)
= 10 / (1 + 4) = 10 / 5 = 2 A.
La diferencia de potencial entre los puntos A
y B, extremos de la carga RL = 4 W
se le denomina tensión de carga VL.
¿ Qué diferencia de potencial tenemos
entre los puntos A y B que son los extremos por un lado de la carga y por
el otro de nuestro generador real ?
Podemos calcularlo de dos maneras:
1ª.- La tension VL
es igual a la f.e.m.E = 10 V. menos la caida de tensión en los extremos
de su resistencia interna Ri.
La caida de tensión o voltaje en Ri
es igual al producto de dicho valor por la corriente I
VRi = Ri x I = 1
x 2 = 2V.
por lo que:
VL = E - VRi = 10
- 2 = 8 V.
2ª.- Aplicando directamente
la ley de OHM en los extremos de RL tenemos que:
VL = RL x I = 4
x 2 = 8 V.
que es el mismo valor, lógicamente, del
que hemos calculado en primer lugar.
Existen otros tipos de cargas distintas a las puramente
resistivas, como son, por ejemplo, los motores.
En éstos, parte de la energía eléctrica consumida
se disipa en forma de calor (pérdida de energía) y otra fracción
de dicha energía se emplea en producir un trabajo mecánico
(trabajo útil).
Para el estudio de los motores, se
pueden suponer éstos como un generador,
cuya fuerza electromotriz se opone al paso de la corriente, por
lo que se le llama FUERZA CONTRAELECTROMOTRIZ,
en serie con una resistencia interna.
La potencia disipada en dicha resistencia interna
será precisamente la potencia perdida en forma de calor, y la potencia
disipada en el generador en forma de fuerza contraelectromotriz, será
la potencia útil transformada en trabajo mecánico.
Ejemplo:
Un generador de E =10 V. de f.e.m. y 0,5
de resistencia interna está conectado a un motor de E' = 8 V. de
f.c.e.m. y 1,5 de resistencia interna
|
0,5 W
1,5 W |
|
|
10 V
|
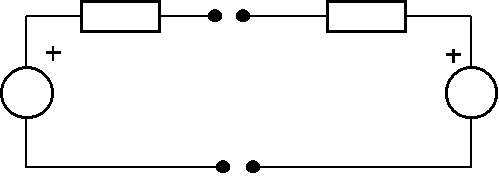
<----------generador real--------->
<-----------motor real--------------->
|
8 V. |
Aquí tenemos el circuito equivalente,
donde observamos que, todos sus elementos están en serie.
Por lo que la corriente I que circula, es
la misma para todos, y será igual al
cociente
entre: la suma de las tensiones de los generadores del circuito
y la suma de las resistencias.- (Ley de OHM).
Como la f.c.e.m. del motor se opone a la f.e.m.
del generador, tendremos que la primera es negativa respecto a la segunda,
con lo que dicha suma de tensiones es igual a 10 - 8 = 2 V.
La suma de todas las resistencias es igual 0,5
+ 1,5 = 2 W .
Por lo que
I = (10 - 8) / (0,5 + 1,5) = 2 / 2 = 1
A.
Veamos las potencias:
Potencia suministrada por el generador: (recordar
que P = V x I)
PG = E x I = 10 x 1 = 10 W.
Potencia disipada en calor en el interior del generador:
(recordar que P = R x I2)
P1 = 0,5 x 12 = 0,5
W.
Potencia disipada en calor en el interior del motor:
P2 = 1,5 x 12 = 1,5
W.
Potencia transformada en trabajo mecánico
del motor:
PW = E' x I = 8 x 1 = 8 W.
En efecto, observar que la potencia suministrada
por el generador es igual a la suma de los otros tres términos de
potencia: (la energía ni se pierde ni se destruye sino que se
transforma)
PG = P1 + P2
+ PW
10 = 0,5 + 1,5 + 8
Un motor ideal será aquel que no tenga
resistencia interna, es decir, que no disipe calor y, por tanto, toda la
energía eléctrica recibida la transforme en trabajo mecánico.
La f.c.e.m. debe ser siempre menor que la f.e.m.
del generador, ya que, en caso contrario, funcionarían al revés:
sería el motor el que entregará energía al generador.(Y
eso no es posible).
|
