El vector (a,2,3) de la dirección de r ha de ser una
combinación lineal de los vectores
u (2,1,3) y v (3,2,5) de dirección de p;
esto es, ha de ser:
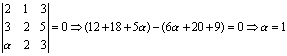
La ecuación de un plano que pasa por (8,-5,2) y direcciones (2,1,3) y (3,2,5) es
:
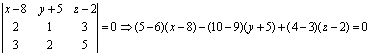
8 - x - y - 5 + z - 2 = 0 =>
x + y -z -1 = 0
La dirección de la normal al plano n = (1,1,-1) deberá ser perpendicular a la
dirección de la recta r (a ,2 ,3), para ello el
producto escalar
de n y r deberá valer cero
n x r = 0.
n x r = a + 2 - 3 = 0 => a = 1